ПРИМЕНЕНИЕ ПАКЕТА MathCAD ПРИ РАСЧЕТЕ МЕХАНИЧЕСКОЙ ЧАСТИ ЛОКОМОТИВОВ
l
Оглавление l Назад l Далее lРасчет перераспределения нагрузок между осями локомотива в режиме тяги
Рассмотрим некоторые задачи из курса “Механическая часть локомотивов”, предлагаемые для решения студентами с использованием пакета MATHCAD. При этом основное внимание обращается на этапы решения с использование ЭВМ:
При движении локомотива в режиме тяги имеет место перераспределение вертикальной статической нагрузки между отдельными колесными парами.
Коэффициент разгрузки колесной пары определяют отношением
![]() ,
,
где
DP - разгрузка колесной пары; Fк - сила тяги одной колесной пары.В проектной и конструкторской практике в качестве критерия оценки тяговых свойств локомотива принято рассчитывать коэффициент использование сцепного веса в следующем виде:
![]() ,
,
где
y - расчетный коэффициент сцепления колес с рельсами.Для расчетов рассматривают максимально разгруженную колесную пару.
Проведем расчет использования сцепного веса для локомотива с осевой формулой 2о-2о (типа ВЛ80) без учета догружающих устройств (рис. 1).
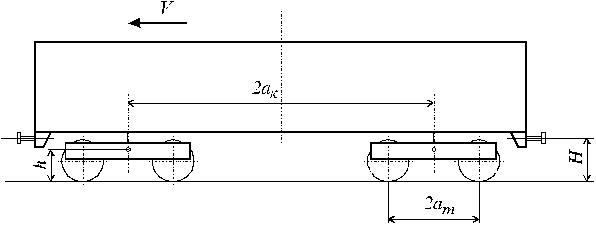
Рис. 1.
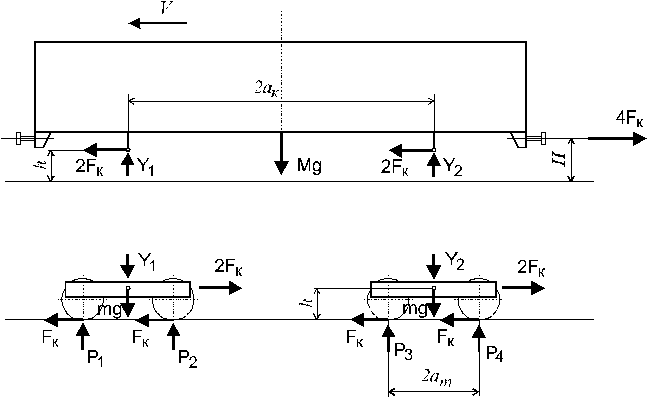
Рис. 2
Рассмотрим схему сил, действующих на локомотив в вертикальной продольной плоскости. Заменим действие частей локомотива друг на друга реакциями в связях (рис. 2).
Составим для кузова и тележек уравнения равновесия сил и моментов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Рассмотрим варианты решения полученной системы с использованием пакета MATHCAD.
Решим полученную систему в пакете MATHCAD с использование уже известных нам операторов Given - Find (пример 6). Обратим внимание, что присвоение исходных данных и начальных приближений независимых переменных предшествует решению системы.
Результаты решения - значения нагрузок от колес на рельсы сохраняются в векторе решения R. Для определения минимального значения нагрузок используем встроенную функцию min.
Студентам рекомендуется составить таблицу соответствия между математическими обозначениями и переменными в программе MATHCAD.
Второй способ решения
Предварительный анализ системы уравнений показывает, что это есть линейная система относительно переменных Y1, Y2, P1, P2, P3, P4. Исходная система уравнений может быть представлена в матричном виде:
A . X = B,
где A - матрица коэффициентов при неизвестных; X - вектор неизвестных; B - вектор свободных членов.
Решение может быть записано в матричном виде:
X = A-1 . B.
В примере 7 приведена программа для пакета MATHCAD.
Следует обратить внимание на формирование матриц и запись операции транспонирования матрицы А (см. табл. 1).
Вектор решения Х содержит: первые два элемента - значения сил между кузовом и тележками, следующие четыре - значения нагрузок от колесных пар на рельсы. Вводится новый вектор R. Для присвоения вектору R результирующих значений нагрузок от колесных пар на рельсы
используется промежуточная переменная и ряд значений (i := 0 ..3). Напомним, что нумерация элементов векторов и матриц начинается с нуля.Студентам предлагается ввести свои данные и проанализировать результаты решения.
l
Оглавление l Назад l Далее l