ПРИМЕНЕНИЕ ПАКЕТА MathCAD ПРИ РАСЧЕТЕ МЕХАНИЧЕСКОЙ ЧАСТИ ЛОКОМОТИВОВ
l
Оглавление l Назад l Далее lРасчет вписывания локомотива в кривую
Рассмотрим решение задачи о вписывании в кривые экипажа тележечного локомотива. Задача является частью расчетов динамических качеств локомотивов.
Цель расчета вписывания в кривые - определение направляющих и боковых сил, отжатия рельсов, положения экипажа в рельсовой колее в зависимости от скорости движения и радиуса кривой.
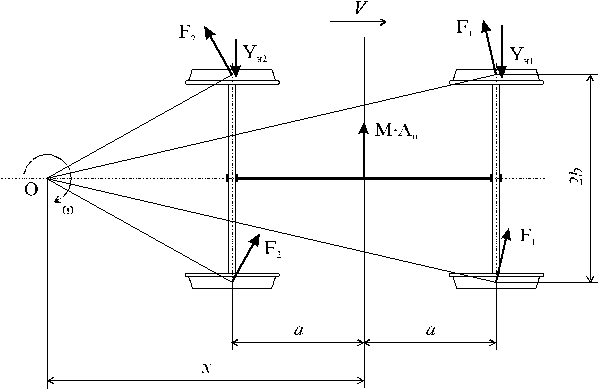
Расчетная схема вписывания в кривую двухосной тележки локомотива представлена на рис. 6.

Рис. 6.
Введены следующие обозначения: 2а - база тележки; 2b - расстояние между кругами катания колес; О - полюс поворота тележки; x - полюсное расстояние; V - скорость движения; M - приведенная масса; F
i - силы трения колес по рельсам; Yн1, Yн2 - направляющие силы, действующие на гребни набегающих колес; Ан - непогашенное ускорение.Схема сил и моментов, действующих на раму тележки, показана на рис. 7.
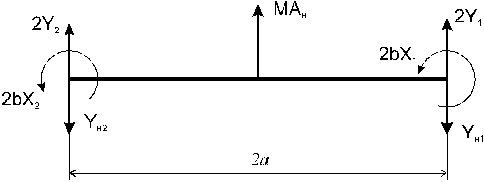
Рис. 7.
Равновесие локомотива при установившемся движении в круговой кривой описывается системой нелинейных алгебраических уравнений. В упрощенном виде не рассматриваются упругие связи колесных пар с рамой тележки и тележек с кузовом. В этом случае математическая модель, описывающая движение тележки в круговой кривой, представляет собой систему двух алгебраических уравнений вида:
![]() ;
;
![]() .
.
Проекции сил трения, входящие в уравнения, можно записать:
![]()
![]()
где Р - нагрузка от колеса на рельс, f - коэффициент трения, x
i - полюсное расстояние i-ой колесной пары,x1 = x + a;
x2 = x - a.
Неизвестными являются полюсное расстояние х, направляющие силы первой и последней оси Yн1
, Yн2, непогашенное центробежное ускорение Aн, т.е. четыре неизвестных. Рассмотрим варианты решения этой задачи.
Для решения системы необходимо избавиться от неопределенности - так называемых “лишних” переменных.
Традиционно задачу решают обратным способом – задаются возможными положениями экипажа в колее и находят соответствующие им величины сил и скорости. Для этого рассматривают дополнительные условия, а именно задают значения полюса поворота и направляющей силы на второй колесной паре при трех положениях экипажа в колее. Для каждого положения фиксируют одну из двух переменных, а вторую изменяют с заданным шагом:
1 - хордовое положение – x = 0, Yн2
2 - промежуточное положение – x = [0…x
max], Yн2 = 0;3 - положение наибольшего перекоса – x =
xmax, Yн2 = [0…-Ymax].При таком подходе уравнения могут быть преобразованы к виду:
Yн1 = f1(x, Yн2);
Aн = f2(x, Yн1, Yн2).
Для ряда заданных значений переменных x и Yн2 находятся неизвестные Yн1
, Aн. Соответствующие точки и есть решение Yн1(Aн). Результаты могут быть представлены в виде Yн1(V), для чего вычисляют V(Aн,R,hp).Один из вариантов решения задачи вписывания локомотива в кривые для промежуточного положения тележки в колее приведен в примере 16.
Студентам предлагается ввести свои данные и по результирующим графикам определить ограничения по безопасной скорости движения в кривой. Для этого из зависимости Yн1
(Aн) определить по заданным ограничениям Aн предельные значения Yн1, а затем по зависимости Yн1(V) определить допустимые значения скорости.
Другой подход к решению задачи вписывания в кривые – решение нелинейной системы численными методами – прямая задача.
Анализ системы показывает, что установка жесткой тележки в колее и силы взаимодействия можно выразить через поперечные перемещения колесных пар относительно оси колеи.
При таком подходе вводятся дополнительные связи, описывающие условия установки колесной пары в колее. Направляющая сила может быть представлена как нелинейная функция от перемещения колесной пары в колее [7]:
![]()
где Cr - жесткость рельса;
h - поперечное перемещение колесной пары относительно оси пути; s - половина свободного зазора в колее.Полюсное расстояние, входящее в определение сил трения колес по рельсам, в свою очередь можно выразить через перемещение колесных пар относительно рельсов:
![]()
С учетом рассмотренных зависимостей получим систему двух уравнений относительно двух неизвестных – перемещений колесных пар относительно рельсовой колее.
Вариант решения задачи приведен в примере 17.
Для решения применена функция MINERR. Начальные приближения выбраны из физических допущений – хордовая установка тележки, при которой колесные пары смещены от оси колеи на величину половины свободного зазора в колее.
Решение проводится для заданных параметров кривой и ряда значений непогашенного ускорения. Результаты – установка колесных пар в колее, направляющие и боковые силы.
Студентам рекомендуется провести анализ используемых нелинейных функций, построить графики. Проверить устойчивость вычислительного процесса при различных начальных приближениях.
l
Оглавление l Назад l Далее l