ПРИМЕНЕНИЕ ПАКЕТА MathCAD ПРИ РАСЧЕТЕ МЕХАНИЧЕСКОЙ ЧАСТИ ЛОКОМОТИВОВ
l
Оглавление l Назад l Далее lРасчет рамы тележки электровоза на вертикальное статическое загружение
Одной из особенностей пакета MATHCAD является возможность выполнения операций над матрицами в естественном виде. Матричные операции суммирования и умножения записываются по тем же правилам, что и арифметические операции. Важно при этом соблюдение размерности матриц. В пакет MATHCAD входят все важнейшие матричные операции: вычисление обратной матрицы, транспонирование, вычисление определителя, нормирование и многие другие.
В примере 15 приведено решение в матричном виде задачи о вертикальном статическом загружении рамы тележки из [5].
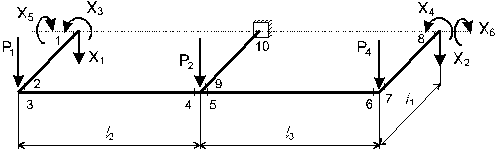
Расчет рам тележек как статически неопределимых систем ведется методом сил (рис.5).
Рис. 5. Расчетная схема статического загружения рамы тележки
Рекомендуется следующий порядок расчета:
а) установление степени статической неопределимости;
б) определение количества “лишних” связей в системе и их удаление, т.е. превращение системы в статически определимую;
в) выбор основной системы;
г) составление канонических уравнений;
д) определение единичных перемещений.
Значения изгибающих моментов в заданных сечениях определим из выражения
Su = Lu.P ,
где
Su - вектор изгибающих моментов;
Lu - матрица влияния изгибающих моментов;
P - вектор нагрузки.
Для рассматриваемого примера имеем: k = 10; m = 3; n = 6;
Su - матрица размера (k x 1);
P - матрица размера (m x 1);
L - матрица влияния усилий в статически неопределимой системе, размера (k x m);
P - вектор-столбец внешней нагрузки с “m” координатами;
X - вектор-столбец “лишних” неизвестных с “n” координатами;
- матрица влияния усилий в основной системе от лишних неизвестных, размера (k x m);
Lo - матрица влияния усилий в основной системе от нагрузки, размера (k x m).
Матрицу влияния изгибающих моментов определим из выражения
,
где
- транспонированная матрица 
;
D-1 - матрица, обратная матрице D;
D - матрица перемещений; 
;
G - матрица погонной податливости
B - блочная квазидиагональная матрица (k x k).
Таким образом, расчет статически неопределимой системы рамы тележки сводится к нахождению линейного преобразования вектора P в вектор Su. Для контроля выводится рассчитанная матрица D и результаты расчета - вектор S.
Студентам рекомендуется ввести свои данные и построить эпюры нагружения по результатам расчета.
l
Оглавление l Назад l Далее l