
УДК 629.4.015:625.031.3
В.Г. Рубан
Решение задачи о вписывании экипажа в кривые с использованием пакета MathCAD
Вестник Ростовского государственного университета путей сообщения , Ростов н/Д, 2000, № 3.
Современное развитие вычислительной техники и программного обеспечения привело к изменению соотношения затрат времени и средств на различных этапах моделирования сложных систем в пользу исследователя. Доля затрат на составление и отладку программ резко сокращается. Развития современных программным продуктов или пакетов, предназначенных для решения различных математических и технических задач, идет по пути создания пользователю максимального удобства при использовании достаточно сложных по внутреннему содержанию средств. В современные интегрированные пакеты включают наряду с большой библиотекой стандартных функций и методов, также средства удобного представления исходных данных и результатов. Считается хорошим тоном иметь большой набор средств отображения результатов в графическом виде. Это, в конечном счете, позволяет исследователю значительно больше времени уделить основному объекту исследования, упростить или свести к неким стандартным действиям работу по созданию отчета.
Вычислительная мощность современных компьютеров в сочетании с предоставлением пользователю всех ресурсов системы, возможностью диалогового режима при решении задачи и анализе результатов позволяют свести к минимуму время решения задачи. Однако внешняя простота использования интегрированных пакетов не снимает с исследователя необходимости обоснования модели, правильного выбора метода решения, анализа и интерпретации полученных результатов.
Одним из ярких представителей современных интегрированных математических пакетов, ориентированных на “непрограммирующих” пользователей является пакет MATHCAD фирмы MathSoft. В настоящее время существует достаточное количество справочной литературы для пользователей пакета MATHCAD. Литература в основном изобилует примерами решения хорошо обусловленных математических задач.
Рассмотрим некоторые вопросы, возникающие при решении нелинейных задач механики с использованием пакета MATHCAD на примере задачи вписывания в кривые участки пути тележечного экипажа локомотива с упругими нелинейными связями.
Задача вписывания экипажа в кривые участки пути относится одной из задач оценки динамических качеств экипажа. В классической постановке по методике проф. К.П. Королева рассматривается установившееся движение в круговой кривой жесткой одиночной тележки с цилиндрическими бандажами колес. Взаимодействие колес с рельсами описывается в рамках кулонова трения. При задании внешних сил и моментов равновесие тележки описывается системой двух нелинейных алгебраических уравнений. Уравнения решаются для трех установок тележки в колее: наибольший перекос, промежуточная, хордовая. При этом для крайних установок тележки ищутся неизвестные направляющие силы, а для промежуточной установки – направляющая сила и полюсное расстояние, определяющее положение тележки в колее. Задачу часто решают обратным способом. Задаются положением экипажа (поскольку полюсное расстояние входит в нелинейности системы) и определяют возможные скорости движения.
При рассмотрении локомотивов с упругими связями необходимо рассматривать связанную систему колесных пар, тележек и кузова локомотива. Результаты, получаемые при решении такой системы, отличаются от классических. Разумеется, при рассмотрении такой системы не может быть речи о расчете множества вариантов установок тележек в колее.
Решение задачи в прямой постановке для локомотива с упругими нелинейными связями приводит к необходимости численного решения системы нелинейных алгебраических уравнений вида
F(X) = 0, где X – вектор независимых переменных, [1].В качестве независимых переменных выбираем обобщенные координаты в системе, равномерно движущейся вдоль кривой – перемещения и угла поворота. Полюсные расстояния тележек и силы взаимодействия колес с рельсами описываются как функции независимых переменных (математические зависимости приведены в тексте рассмотренного ниже примера). Силы и моменты в связях тележек с кузовом локомотива должны быть также выражены через обобщенные координаты.

Рис. 1. Зависимость направляющей силы от перемещения колесной пары
Для общности описания условий установки колесной пары в колее вводится нелинейная функция направляющей силы в зависимости от перемещения колесной пары относительно центра колее. Вариант реализации этой функции в пакете MATHCAD представлен на рис. 1. На графике показаны границы свободного зазора в колее, внутри которого направляющая сила равна нулю.
Такой подход наилучшим образом отвечает требованиям формализации задачи при использовании численных методов [2].
Рассмотрим вариант реализации математической модели в пакете MATHCAD.
Для решения систем нелинейных алгебраических уравнений в пакете предлагаются две функции: FIND, MINERR. Обе функции доставляют решение системе уравнений при заданном векторе начальных приближений. Разработчики пакета указывают, что решение производится методом Левенберга-Марквардта. Обе функции находят ближайшее решение. Кроме того, функция MINERR минимизирует ошибку решения. Как показывает опыт, эта функция чаще находит решение для систем большой размерности. Для проверки решений рекомендуется
задать различные начальные приближения независимой переменной. Отсутствие решения не означает, что решения нет. Чаще всего следует изменить начальные приближения. Поэтому, для функций, имеющих так называемую область притяжения решения, остается проблема выбора вектора начальных приближений. Выходная информация при любом варианте отсутствия решения или при некорректном использовании в уравнениях нелинейных функций ограничена сообщением типа “решение не может быть найдено”.Последовательность действий при решении задачи в пакете MATHCAD имеет много общего с программированием на других языках высокого уровня. В начале определяются исходные данные и функции пользователя, далее формируется блок решения системы уравнений, проводится решения для ряда заданных параметров, и в завершении выводятся графики результатов. Особенностью решения в пакете MATHCAD является совмещение расчетных формул, комментариев, процесса решения и результатов в одном документе.

Рис. 2. Фрагмент программы, описывающий ввод данных
Для подсистемы, описывающей равновесие двухосной тележки в кривой под действием заданного момента сил от кузова, программа для MATHCAD выглядит следующим образом (рис. 2 – 4).
Несомненным плюсом пакета MATHCAD является представление формул в привычном математическом виде. Это позволяет уменьшить объем формул в поясняющем документе. Все вычисления открыты, а логика программы легко прослеживается.

Рис.3. Фрагмент программы, описывающий нелинейные функции

Рис. 4. Фрагмент программы, описывающий блок решения уравнений
Начальные приближения приняты, исходя из физического смысла задачи: первая колесная пара набегает на наружный рельс, вторая – находится на оси кривой (промежуточная установка тележки). Наилучшие результаты получены при решении с использованием функции MINERR, как менее чувствительной к начальным приближениям.
Результаты решения представлены на графиках зависимостей перемещений колесных пар (рис. 5а), направляющих и боковых сил (рис. 5б) от непогашенного центробежного ускорения An.
|
а) перемещение колесных пар |
б) направляющие и боковые силы |
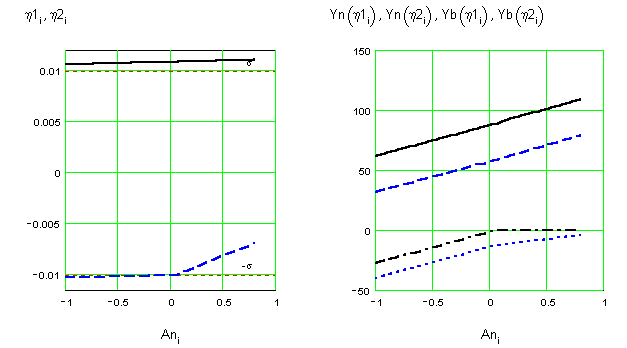
Рис. 5. Фрагмент программы, вывод результатов
Из приведенных на рис. 5 результатов видно, при непогашенном ускорении An=0,08 м/с
2 происходит переход от положения наибольшего перекоса в промежуточное положение. Таким образом, реализовано решение задачи в прямой постановке – определение положения экипажа в кривой и сил взаимодействия его с рельсами при заданном внешнем воздействии.При изменении исходные данные в документе MATHCAD автоматически вычисляются и выводятся новые результаты. Это позволяет создавать “живые” документы, в которых все компоненты моделирования – описание, данные, метод и результаты взаимосвязаны и работоспособны.
Усложнение математической модели при переходе от рассмотрения одиночной тележки к локомотиву с нелинейными связями, приводит в свою очередь к увеличению количества уравнений в системе и введению новых функций пользователя, описывающих связи. Для тележечного локомотива это функции: возвращающих устройств, определяющих поворот и относ тележки; упругих связей тележек и колесных пар; нелинейного профиля поверхности катания колес; нелинейной характеристики трения.
Поскольку в пакете MATHCAD при создании функций пользователя отсутствует механизм индексации функций или описание вложенных блоков, то при создании сложных функций требуется передавать большое количество параметров в качестве аргументов, или включать уравнения связей в качестве дополнительных условий в решаемую систему уравнений. Размерность системы возрастает, а наглядность такой модели теряется.
Кроме того, следует учесть, что при написании программ для MATHCAD система последовательно просматривает вводимые выражения, контролируя правильность синтаксиса. Это облегчает процесс ввода. Однако, когда возникают ошибки вычисления, то сообщения системы очень скудны, и невозможно провести трассировку ошибок, как это возможно при программировании для большинства алгоритмических языков высокого уровня.
Как показал опыт использования пакета MATHCAD для решения задач нелинейных задач механики, в частности, задач вписывания в кривые различных типов экипажей, отработку моделей следует проводить “от простого к сложному”, проверяя промежуточные результаты. В качестве ограничения размерности модели можно предложить показатель “удобочитаемости” документа MATHCAD. Иначе говоря, размерность решаемой задачи можно поставить в зависимость от подготовленности пользователя. Для любителей писать закрученные программы всегда есть альтернатива обратиться к программированию на других языках, а MATHCAD использовать, как инструмент предварительного анализа для быстрого получения результата, и в качестве удобной среды общения исследователей.
Список использованных источников