Моделирование в системе SIMULINK

Вертикальные колебания экипажа ЭПС
Математическая модель вынужденных колебаний двухмассовой системы
Модель вынужденных колебаний двухмассовой системы в системе Simulink
Использование подсистем
Использование подпрограмм пользователя

Для моделирования поведения динамических систем, к которым относятся экипажи подвижного состава, используются ЭВМ. Существует большое количество алгоритмических языков, на которых может быть выполнено решение задачи. Выбор того или иного языка программирования зависит от многих условий. Часто решающую роль оказывает удобство программирования, наличие проверенных математических методов, легкость представления результатов моделирования. Такими особенностями обладает пакет MATLAB, содержащий в своем составе инструмент визуального моделирования SIMULINK.

SIMULINK сочетает в себе наглядность аналоговых машин и точность цифровых вычислительных машин. SIMULINK обеспечивает пользователю доступ ко всем возможностям пакета MATLAB, в том числе к большой библиотеке численных методов.

Подготовка задачи для моделирования в SIMULINK проводится в следующей последовательности:

Выбор расчетной схемы.
Составление системы уравнений, описывающих исследуемый процесс.
Приведение системы к виду, удобному для решения (разрешение относительно старших производных).
Определение начальных условий.
Составление структурной схемы.
Моделирование возмущающих функций.
Определение исходных данных.
Составление модели в среде SIMULINK.
Включение средств визуализации.
Тестирование.
Решение.
Анализ результатов.
Отчет.

Ниже рассмотрены примеры моделирования в среде SIMULINK на простых примерах.

Вертикальные колебания экипажа ЭПС

Математическая модель вынужденных колебаний двухмассовой системы

Для исследования влияния основных параметров экипажа на вертикальные колебания используют упрощенную модель с двумя степенями свободы, в которой две массы связаны упругими и диссипативными связями (рис.1). Такая модель описывает вертикальные колебания рельсовых экипажей с двухъярусным подвешиванием: магистральных локомотивов (электровозов и тепловозов) и пассажирских вагонов.

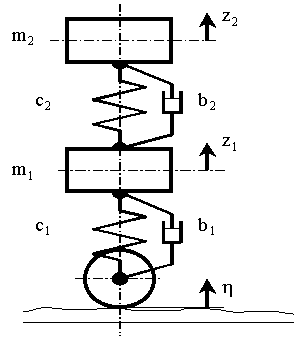
Рис.1. Расчетная схема

Уравнения движения рассматриваемой системы при наличии возмущения со стороны пути описывается следующими дифференциальными уравнениями:

;

(1)

В уравнениях (1) введены следующие обозначения:

m₁ – обрессоренная масса тележки;

m₂ – масса кузова, приведенная к одной тележке;

с₁, b₁ – жесткость и демпфирование в первом ярусе подвешивания;

с₂, b₂ – жесткость и демпфирование во втором ярусе подвешивания;

h(t) – возмущение со стороны пути;

– обобщенные координаты и их производные по времени:

Преобразуем уравнения движения к виду:

;

(2)

В качестве возмущения используем неровность проф. Н.Н.Кудрявцева. Неровность хорошо описывает изменение прогиба вдоль рельсового звена. Модель неровности представляет собой сумму полуволны синусоиды частотой w и трех полуволн синусоиды частотой 3w, уложенные на длине рельсового звена L. Амплитуды неровностей A₁ A₂ выбираются в зависимости от типа и состояния пути.

(3)

где

- частота возмущения;

V - скорость движения.

Построим описанную выше модель в среде SIMULINK.

Модель вынужденных колебаний двухмассовой системы в системе Simulink

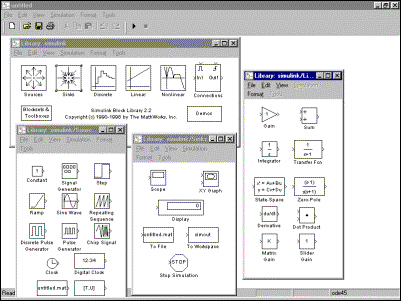
При запуске SIMULINK открываются два окна:

- пустое рабочее окно – заготовка для создания новой модели (untitled);

- окно библиотеки SIMULINK, содержащей наборы основных разделов (Library: simulink).

Далее можно раскрыть необходимые разделы библиотеки SIMULINK (рис. 2).

Рис. 2. Пример начала работы в SIMULINK

Поскольку моделируемая система довольно проста, покажем реализацию модели одного уровня (без вложенных подсистем).

Процесс построения модели в системе Simulink представляет последовательность выбора необходимых блоков из соответствующих библиотек, и соединение их связями.

Обычно для моделирования динамической системы используют уравнения движения в виде (2).

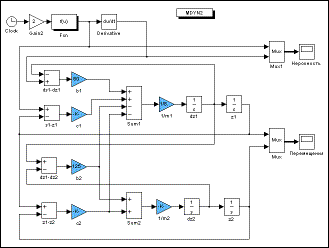
Построение модели каждого уравнения начинаем с сумматора, имеющего столько входов, сколько членов содержит правая часть уравнение. Для первого уравнения это сумматор Sum1 (рис. 3). Входы сумматора могут иметь как положительное значение, так и отрицательное (рис. 4). Используемые блоки рекомендуется именовать для облегчения последующей проверки и анализа.

Рис. 3. Блок-схема модели

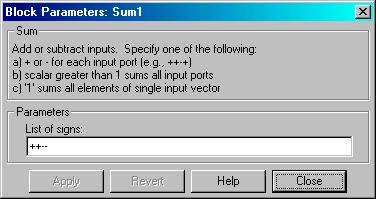
Рис. 4. Настройка сумматора

К выходу сумматора подключаем линейный преобразователь (множитель 1/m1), на выходе которого получаем значение второй производной. Далее включаем последовательно два интегратора (dz1, z1), на выходе которых получаем значения первой производной и самой переменной.

В нашем случае имеем два уравнения, соответственно процесс повторяем для второго уравнения.

Далее устанавливаем связи между входами и выходами соответствующих блоков, применяя, где необходимо, дополнительные линейные преобразователи и сумматоры.

Для моделирования возмущения используем функциональный блок Fcn, в котором в аналитическом виде запишем зависимость перемещения неровности от времени. Блок имеет вход, на который через линейный преобразователь подается от "таймера" независимая переменная - время.

Для вычисления производной перемещения неровности используется блок дифференцирования.

После установки всех связей определяем необходимые коэффициенты в используемых преобразователях.

Для моделирования использованы следующие исходные данные:

амплитуда первой гармоники неровности	A₁ = 0.005	м;
амплитуда второй гармоники неровности	A₂ = 0.002	м;
длина рельсового звена	L = 25	м;
масса первого тела	m₁ = 8.82	т;
жесткость первого яруса	c₁ = 7000	кН/м;
демпфирования первого яруса	b₁ = 60	кН с/м;
масса второго тела	m₂ = 25.8	т;
жесткость второго яруса	c₂ = 2600	кН/м;
демпфирования второго яруса	b₂ = 125	кН с/м.

Зададим значения коэффициентов в соответствующих блоках (рис. 5).

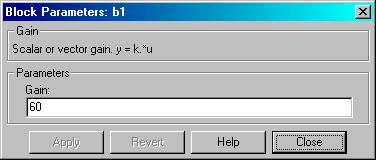
Рис. 5. Задание коэффициента линейного преобразователя

Настроим интеграторы, зададим нулевые начальные условия (рис. 6).

Установим параметры интегрирования через меню (рис. 7).

Начало интегрирования – 0, конец интегрирования – 10. Используем метод ODE45 с переменным шагом интегрирования.

В соответствие с формулой (3) запишем функцию возмущения в блоке Fcn (рис. 8).

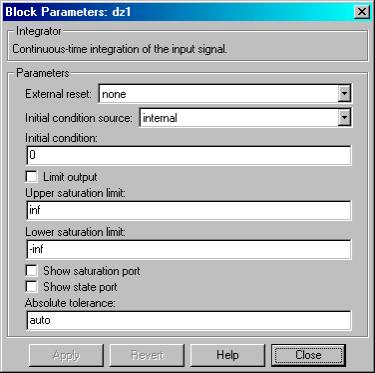
Рис. 6. Панель настойки интегратора

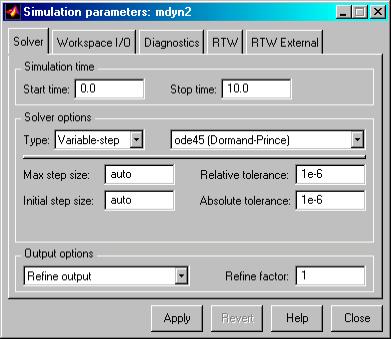
Рис. 7. Параметры интегрирования

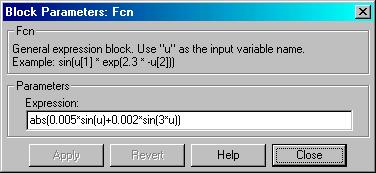
Рис. 8. Функция возмущения

Для наблюдения за процессами в модели установим "осциллограф" - блок Scope, обозначенный "Перемещения", для отображения изменения переменных во времени.

Модель готова.

Приступаем к тестированию.

Проведем моделирование для заданных исходных данных.

Результаты моделирования представим в графическом виде (рис. 9).

При тестировании оцениваем соответствие модели поставленной задачи.

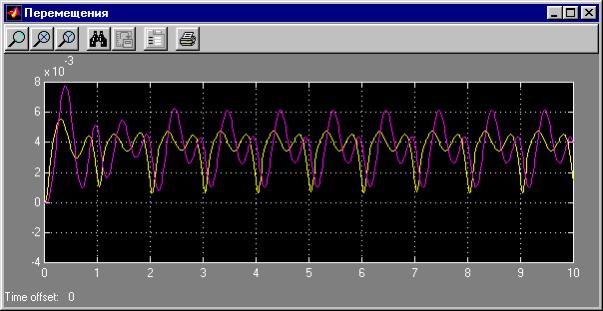
Рис. 9. Результаты моделирования – перемещения

Использование подсистем

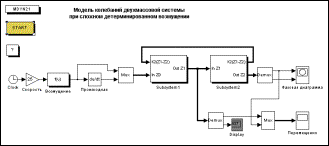
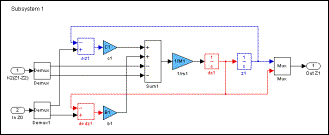
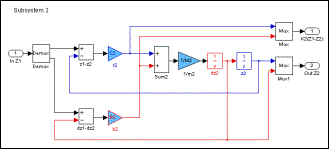
Для моделирования простых систем достаточно использовать подход описанный выше. При увеличении размерности для увеличения наглядности и удобства отладки выделяют логические блоки – подсистемы. SIMULINK поддерживает многоуровневые системы. Для вложенных подсистем используют блок Subsystem (рис. 10). При раскрытии такого блока выводится окно с моделью соответствующей подсистемы (рис. 11, 12). Для передачи входных и выходных переменных используются так называемые порты подсистемы входные и выходные. В приведенном примере используются многоканальные порты – через один порт передается переменная и ее производная. Для создания «сложной переменной» (на блок-схеме такие переменные показаны жирными линиями) применяется блок Mux, для разделения – блок Demux.

Для большой разветвленной модели предпочтительно исходные данные собрать в одном месте, что облегчает настройку при исследовании влияния параметров системы. Один из вариантов – использование модуля присвоения начальных значений переменным MATLAB и использование в модулях SIMULINK имен этих переменных. В модели, показанной на рис. 10, в модуле START используется ссылка на подпрограмму в которой осуществляется присвоение начальных значений (рис. 13).

Рис. 10. Модель системы

Рис. 11. Подсистема, описывающая колебания первого тела

Рис. 12. Подсистема, описывающая колебания второго тела

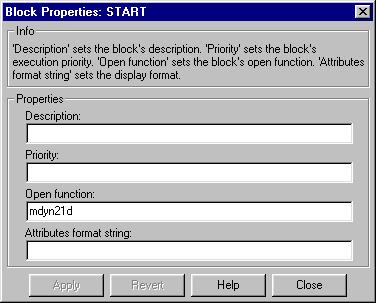
Рис. 13. Настройка запускающей программы

Подпрограмма задания начальных значений – обычный m-файл. Для данного примера в файле MDYN21.m задаются следующие значения:

% MDYN21
% Start programm
%
echo on
A1=0.005;
A2=0.002;
L=25;
p=pi/L;
M1=8.82;
C1=7000;
B1=60;
M2=25.8;
C2=2600;
B2=125;
echo off
x0 = [0; 0; 0; 0;];
[t,x]=sim('mdyn21',10,simset('InitialState',x0));

В приведенном тексте подпрограммы знак "точка с запятой" в конце строки запрещает вывод значений переменных.

Для отображения введенных данных применены операторы «echo on – echo off». Выделенный фрагмент подпрограммы выводится в управляющее окно MATLAB (рис 14).

Для изменения исходных данных используется текстовый редактор.

Запуск моделирующей программы в этом примере осуществляется двойным нажатием на блок START.

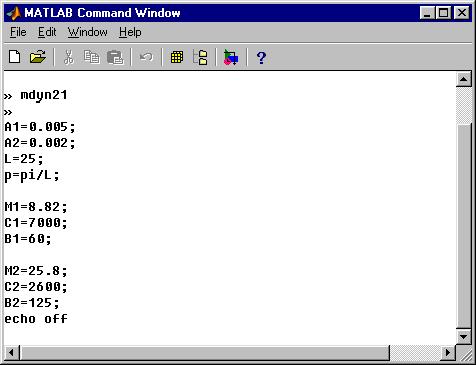
Рис. 14. Вывод в окне управляющей программы MATLAB

Добавим в модель информационный блок, содержащий краткое описание модели – блок Info, обозначенный символом «?». Содержание блока показано на рис. 15.

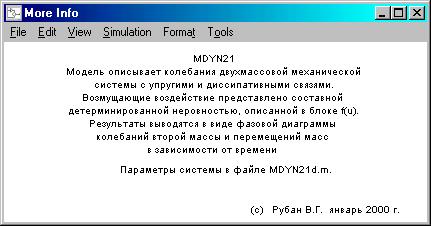
Рис. 15. Информационный блок

Для отображения фазовой диаграммы введем блок отображения XY_Graph, обозначенный на блок-схеме "фазовая диаграмма". Результаты вывода показаны на рис. 16.

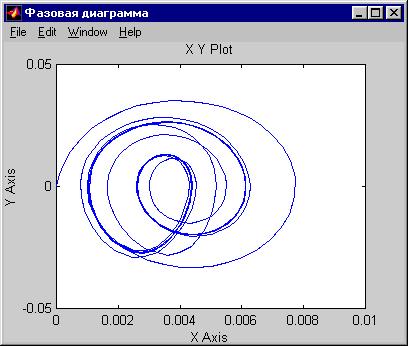
Рис. 16. Результаты моделирования – фазовая диаграмма

Использование подпрограмм пользователя

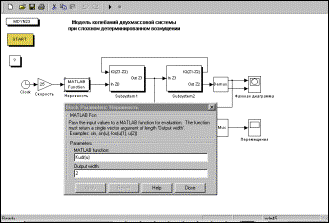
Для расширения возможностей моделирования в среде SIMULINK предусмотрена возможность подключения подпрограмм пользователя написанных на языке MATLAB. В предыдущей модели заменим функции неровности модулем "MATLAB Function" - "Неровность". Модель определяет ссылку на подпрограмму пользователя, в которой описана функция неровности от пути и ее производная (рис. 17). Такой подход позволяет использовать проверенные модули как при программировании в пакете MATLAB, так и при моделировании в среде SIMULINK.

Рис. 17. Модель и настройка блока функции MATLAB

Рассмотренные примеры не претендуют на полноту описания возможностей пакета MATLAB и среду визуального моделирования SIMULINK. Для изучения рекомендуем специальную литературу и руководство пользователя.